Sistem Bilangan
Sistem Bilangan atau Number System adalah Suatu cara untuk mewakili besaran dari suatu item fisik. Sistem Bilangan menggunakan suatu bilangan dasar atau basis (base / radix) yang tertentu. Dalam hubungannya dengan komputer, ada 4 Jenis Sistem Bilangan yang dikenal yaitu : Desimal (Basis 10), Biner (Basis 2), Oktal (Basis 8) dan Hexadesimal (Basis 16). Berikut penjelesan mengenai 4 Sistem Bilangan ini :
1. Desimal (Basis 10)
Desimal (Basis 10) adalah Sistem Bilangan yang paling umum digunakan dalam kehidupan sehari-hari. Sistem bilangan desimal menggunakan basis 10 dan menggunakan 10 macam simbol bilangan yaitu : 0, 1, 2, 3, 4, 5, 6, 7, 8 dan 9. Sistem bilangan desimal dapat berupa integer desimal (decimal integer) dan dapat juga berupa pecahan desimal (decimal fraction).
Untuk melihat nilai bilangan desimal dapat digunakan perhitungan seperti berikut, misalkan contoh bilangan desimal adalah 8598. Ini dapat diartikan :
Dalam gambar diatas disebutkan Absolut Value dan Position Value. Setiap simbol dalam sistem bilangan desimal memiliki Absolut Value dan Position Value. Absolut value adalah Nilai Mutlak dari masing-masing digit bilangan. Sedangkan Position Value adalah Nilai Penimbang atau bobot dari masing-masing digit bilangan tergantung dari letak posisinya yaitu bernilai basis di pangkatkan dengan urutan posisinya. Untuk lebih jelasnya perhatikan tabel dibawah ini.
Dengan begitu maka bilangan desimal 8598 bisa diartikan sebagai berikut :
Sistem bilangan desimal juga bisa berupa pecahan desimal (decimal fraction), misalnya : 183,75 yang dapat diartikan :
2. Biner (Basis 2)Biner (Basis 2) adalah Sistem Bilangan yang terdiri dari 2 simbol yaitu 0 dan 1. Bilangan Biner ini di populerkan oleh John Von Neumann. Contoh Bilangan Biner 1001, Ini dapat di artikan (Di konversi ke sistem bilangan desimal) menjadi sebagai berikut :
Position Value dalam sistem Bilangan Biner merupakan perpangkatan dari nilai 2 (basis), seperti pada tabel berikut ini :
Berarti, Bilangan Biner 1001 perhitungannya adalah sebagai berikut :
3. Oktal (Basis 8)
Oktal (Basis 8) adalah Sistem Bilangan yang terdiri dari 8 Simbol yaitu 0, 1, 2, 3, 4, 5, 6, 7. Contoh Oktal 1024, Ini dapat di artikan (Di konversikan ke sistem bilangan desimal) menjadi sebagai berikut :
Position Value dalam Sistem Bilangan Oktal merupakan perpangkatan dari nilai 8 (basis), seperti pada tabel berikut ini :
Berarti, Bilangan Oktal 1022 perhitungannya adalah sebagai berikut :
Position Value dalam Sistem Bilangan Oktal merupakan perpangkatan dari nilai 8 (basis), seperti pada tabel berikut ini :
Berarti, Bilangan Oktal 1022 perhitungannya adalah sebagai berikut :
4. Hexadesimal (Basis 16)
Hexadesimal (Basis 16), Hexa berarti 6 dan Desimal berarti 10 adalah Sistem Bilangan yang terdiri dari 16 simbol yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15). Pada Sistem Bilangan Hexadesimal memadukan 2 unsur yaitu angka dan huruf. Huruf A mewakili angka 10, B mewakili angka 11 dan seterusnya sampai Huruf F mewakili angka 15.
Contoh Hexadesimal F3D4, Ini dapat di artikan (Di konversikan ke sistem bilangan desimal) menjadi sebagai berikut :
Position Value dalam Sistem Bilangan Hexadesimal merupakan perpangkatan dari nilai 16 (basis), seperti pada tabel berikut ini :
Berarti, Bilangan Hexadesimal F3DA perhitungannya adalah sebagai berikut :
Cara Menghitung Konversi Sistem Bilangan
Sistem bilangan atau numbering system merupakan angka yang digunakan sebagai alat bantu untuk menghitung atau menuliskan sebuah nilai. Hal ini dapat dianalogikan pada sebuah komputer. Komputer terdiri dari transistor yang tergabung dalam sebuah microchips. Microchips digunakan untuk menyampaikan informasi. Sedangkan transistor hanya mengenali dua buah status yaitu nyala dan mati. Dua status ini dapat diterjemahkan dalam bilangan biner yang terdiri dari 2 basis, 0(mati) dan 1(nyala).
Manusia memiliki 10 jari, sehingga untuk mempermudah perhitungan, manusia berhitung dengan sistem bilangan dengan basis 10, yaitu desimal. Bilangan desimal terdiri dari 1,2,3,4,5,6,7,8,9 dan 0. Selain kedua sistem bilangan tersebut, seringkali manusia menggunakan sistem bilangan lain yaitu basis 8 (Oktal), dan Basis 16 (Hexadesimal). Antar basis terdapat angka yang sama dan ada yang tidak. Agar mudah membedakannya maka diberikan penambahan besar basis di akhir angka. Contoh 1101(2) untuk biner, 1101(10) untuk desimal, 1321(8) untuk oktal, dan 1321(16) untuk hexadesimal.
1. Bilangan Biner
Bilangan biner terdiri dari dua basis 0 dan 1. Supaya mempermudah perhitungan, bilangan biner diterjemahkan ke basis 10 terlebih dahulu. Dalam menghitung basis ini ke desimal menggunakan penjumlahan 2 pangkat. Contoh terjemahkan bilangan biner 1101(2) ke desimal:
28
|
27
|
26
|
25
|
24
|
23
|
22
|
21
|
20
|
256
|
128
|
64
|
32
|
16
|
8
|
4
|
2
|
1
|
| 1 | 1 | 0 | 1 | Desimal |
| 23 x 1 | 22 x 1 | 21 x 0 | 20 x 1 | = (8+4+0+1) = 13(10) |
Sehingga 1101(2) = 13(10)
Contoh bilangan biner :
| 0000 0000 | 0 |
| 0000 0001 | 1 |
| 0000 0010 | 2 |
| 0000 0011 | 3 |
| 0000 0100 | 4 |
| 0000 0101 | 5 |
| 0100 0101 | 133 |
| 1111 1111 | 511 |
2. Bilangan Oktal
Bilangan oktal terdiri dari delapan basis 0,1,2,3,4,5,6, dan 7. Cara perhitungannya sama dengan binary. Perbedaannya dalam basis ini menggunakan penjumlahan 8 pangkat. Contoh terjemahkan bilangan oktal 1321(8) ke desimal:
| 83 | 82 | 81 | 80 |
| 512 | 64 | 8 | 1 |
| 1 | 3 | 2 | 1 | Desimal |
| 83 x 1 | 82 x 3 | 81 x 2 | 80 x 1 | = (512+192+16+1)
= 721(10)
|
Sehingga 1321(8) = 721(10)
3. Bilangan Hexadesimal
Bilangan hexadesimal terdiri dari 16 basis yaitu, 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E, dan F. Huruf pada hexadecimal diterjemahkan kelanjutan dari angkanya. Pada huruf A dihitung 10, huruf B dihitung 11, dan seterusnya sampai huruf F. Berbeda dengan basis lainnya, cara penulisan basis ini diawali dengan 0x. Dalam menghitung basis ini ke desimal menggunakan penjumlahan 16 pangkat. Contoh terjemahkan bilangan hexadecimal 19F(16) ke desimal:
163
|
162
|
161
|
160
|
4096
|
256
|
16
|
1
|
1
|
9
|
F
|
Desimal
|
162 x 1
|
161 x 9
|
160 x 15
|
= (256+144+15)
= 415(10)
|
Sehingga 19F(16) = 415(10)
4. Bilangan Desimal
Bilangan desimal terdiri dari 10 basis, 1,2,3,4,5,6,7,8,9 dan 0. Selain basis lain yang diterjemahkan ke bilangan desimal. Bilangan desimal juga dapat diterjemahkan ke basis lain. Basis lain diterjemahkan menggunakan hasil jumlah dari x pangkat. Kebalikannya, untuk mengubah bilangan desimal ke basis lain, menggunakan pembagian.
a. Desimal ke Biner
Dalam menerjemahkan bilangan desimal ke biner, bilangan desimal dibagi dengan 2. Bilangan dibagi hingga habis atau hasilnya sama dengan 0. Jika terdapat sisa pada pembagian, maka bernilai 1. Jika tidak terdapat sisa pada pembagian maka bernilai 0. Contoh terjemahkan bilangan 251(10)
Decimal
|
Habis dibagi / tidak
|
Biner
|
251 / 2 = 125
|
sisa
|
1
|
125 / 2 = 62
|
sisa
|
1
|
62 / 2 = 31
|
tidak sisa
|
0
|
31 / 2 = 15
|
sisa
|
1
|
15 / 2 = 7
|
sisa
|
1
|
7 / 2 = 3
|
sisa
|
1
|
3 / 2 = 1
|
sisa
|
1
|
1 / 2 = 0
|
sisa
|
1
|
Dalam penulisannya, hasil pembagian pertama berada di ujung kiri, terurut kearah kanan. Sehingga 251(10) = 1111 1011(2)
b. Desimal ke Oktal
Dalam menerjemahkan bilangan desimal ke oktal, bilangan desimal dibagi dengan 8. Bilangan dibagi hingga habis atau hasilnya sama dengan 0. Jika terdapat sisa pada pembagian, maka nilai tersebutlah yang ditulis. Contoh terjemahkan bilangan 251(10)
Decimal
|
Sisa Pembagian
|
Oktal
|
251 / 8 = 31
|
3
|
3
|
31 / 8 = 3
|
7
|
7
|
3 / 8 = 0
|
3
|
3
|
Dalam penulisannya, hasil pembagian pertama berada di ujung kiri, terurut kearah kanan. Sehingga 251(10) = 373(8)
c. Desimal ke Hexadesimal
Dalam menerjemahkan bilangan desimal ke hexadesimal, bilangan desimal dibagi dengan 16. Bilangan dibagi hingga habis atau hasilnya sama dengan 0. Jika terdapat sisa pada pembagian, maka nilai tersebutlah yang ditulis. Contoh terjemahkan bilangan 251(10) ke hexadesimal:
Decimal
|
Sisa Pembagian
|
Hexadesimal
|
| 251 / 16 = 15 | 11 | B |
| 15 / 16 = 0 | 15 | F |
Dalam penulisannya, hasil pembagian pertama berada di ujung kiri, terurut kearah kanan. Sehingga 251(10) = FB(16)
Pengertian Dan Jenis Gerbang Logika (Logic Gates)
1. PENGERTIAN GERBANG LOGIKA (LOGIC GATES)
Gerbang Logika (Logic Gates) adalah sebuah entitas untuk melakukan pengolahan input-input yang berupa bilangan biner (hanya terdapat 2 kode bilangan biner yaitu, angka 1 dan 0) dengan menggunakan Teori Matematika Boolean sehingga dihasilkan sebuah sinyal output yang dapat digunakan untuk proses berikutnya.
Pengertian Gerbang Logika
"Gerbang logika atau gerbang logik adalah suatu entitas dalam elektronika dan matematika Boolean yang mengubah satu atau beberapa masukan logik menjadi sebuah sinyal keluaran logik. Gerbang logika terutama diimplementasikan secara elektronis menggunakan diode atau transistor, akan tetapi dapat pula dibangun menggunakan susunan komponen-komponen yang memanfaatkan sifat-sifat elektromagnetik (relay), cairan, optik dan bahkan mekanik."
2. JENIS-JENIS GERBANG LOGIKA (LOGIC GATES)
7 jenis gerbang logika :
- Gerbang AND : Apabila semua / salah satu input merupakan bilangan biner (berlogika) 0, maka output akan menjadi 0. Sedangkan jika semua input adalah bilangan biner (berlogika) 1, maka output akan berlogika 1.
- Gerbang OR : Apabila semua / salah satu input merupakan bilangan biner (berlogika) 1, maka output akan menjadi 1. Sedangkan jika semua input adalah bilangan biner (berlogika) 0, maka output akan berlogika 0.
- Gerbang NOT : Fungsi Gerbang NOT adalah sebagai Inverter (pembalik). Nilai output akan berlawanan dengan inputnya.
- Gerbang NAND : Apabila semua / salah satu input bilangan biner (berlogika) 0, maka outputnya akan berlogika 1. Sedangkan jika semua input adalah bilangan biner (berlogika) 1, maka output akan berlogika 0.
- Gerbang NOR : Apabila semua / salah satu input bilangan biner (berlogika) 1, maka outputnya akan berlogika 0. Sedangkan jika semua input adalah bilangan biner (berlogika) 0, maka output akan berlogika 1.
- Gerbang XOR : Apabila input berbeda (contoh : input A=1, input B=0) maka output akan berlogika 1. Sedangakan jika input adalah sama, maka output akan berlogika 0.
- Gerbang XNOR : Apabila input berbeda (contoh : input A=1, input B=0) maka output akan berlogika 0. Sedangakan jika input adalah sama, maka output akan berlogika 1.
Karnaugh Map Beserta Penjelasannya
Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah variable dan fungsi logika atau jumlah inputan dari rangkaian logika yang sedang kita hitung.
| Rumus untuk menentukan jumlah kotak pada K-Map adalah 2^n yang manan adalah banyaknya variabel / inputan. |
Langkah – langkah pemetaan K-Map secara umum :
- Menyusun aljabar Boolean terlebih dahulu
- Menggambar rangkaian digital
- Membuat Table Kebenarannya
- Merumuskan Tabel Kebenarannya
- Lalu memasukkan rumus Tabel Kebenaran ke K-Map (Kotak-kotak)
Penyederhanaan Dua Variabel
Catatan : Bar = ‘
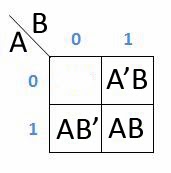
Tabel dari K-Map 2 variabel adalah seperti dibawah ini
Contoh Soal :
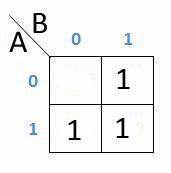
H = AB + A’B+AB’
Maka cara pengerjaanya seperti dibawah ini
Bar (‘) atau aksen biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar aksen.
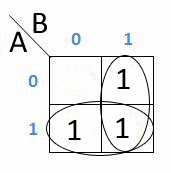
Dan dapat dipermudah lagi menjadi dibawah ini :
Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya:
Karena kolom ber angka 1 dan baris ber angka 1 memenuhi setiap garisnya, maka dapat disimpulkan kalau H = AB + A’B+AB’ K-Map nya adalah AB/BA
Penyederhanaan Tiga Variabel
Catatan : Bar = ‘
Tabel dari K-Map 3 variabel adalah seperti dibawah ini
Contoh Soal
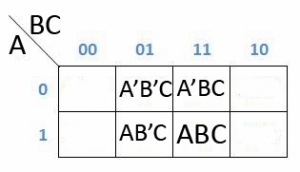
H = ABC + A’BC+A’B’C+AB’C
Maka cara pengerjaanya seperti dibawah ini
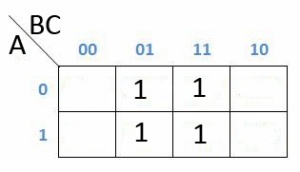
Dan dapat dipermudah lagi menjadi dibawah ini
Sekarang kita lihat, karena yang memenuhi setiap kotaknya adalah baris 01 dan 11 sedangkan simbol 01 artinya adalah (B’C) dan 11 artinya adalah (BC) dan simbol yang tidak ada aksen nya hanya C, maka H = ABC + A’BC+A’B’C+AB’C adalah C.
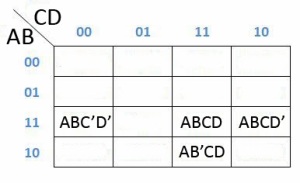
Penyederhanaan 4 variabel
Catatan : Bar = ‘
Tabel dari K-Map 4 variabel adalah seperti dibawah ini :
Contoh Soal
H = ABCD + ABCD’+AB’CD+ABC’D’
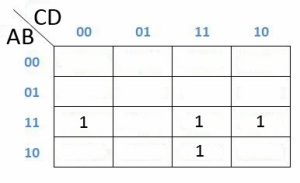
Maka cara pengerjaanya seperti dibawah ini
Dan dapat dipermudah lagi menjadi dibawah ini :
Karena yang ada angka 1 nya ada di kolom dan baris 1100, 1111, 1110 dan 1011, yaitu AB, ABCD, ABC dan ACD maka jika kita eliminasi dengan cara mengambil huruf yang sama saja menjadi AB + ABC + ACD.
